2012年岩土工程师考试基础知识模拟试题:高等数学(单项选择题4)
发布时间:2012-07-25 共1页
高等数学(单项选择题4)
| 一、单项题的备选项中只有一个最符合题意,错选、多选均不得分。 |
| 1.设a、b、c均为非零向量,则与a不垂直的向量是: |
正确答案:D 解题思路:提示:非零向量a⊥b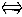 a·b=0,把a分别和A、B、C、D作数量积得,向量a与A、B、C的数量积均为0,D与a的数量积计算如下 a·b=0,把a分别和A、B、C、D作数量积得,向量a与A、B、C的数量积均为0,D与a的数量积计算如下[a+(a×b)×a]·a=a·a+(a×b)×a·a=|a| .gif) ≠0 ≠0 |
|
|
2.曲面x.gif) /3+y /3+y.gif) +z +z.gif) /5=1上M点的法向量与三个坐标轴正向的夹角相等,M点的坐标有两个答案分别是: /5=1上M点的法向量与三个坐标轴正向的夹角相等,M点的坐标有两个答案分别是: |
正确答案:C 解题思路:提示:设M(x ,y ,y ,z ,z )为曲面上点,求过M的法线向量, )为曲面上点,求过M的法线向量,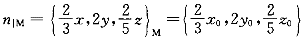 ,计算出方向余弦 ,计算出方向余弦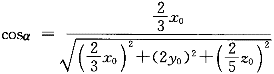 、 、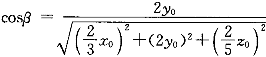 、 、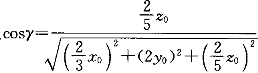 ,因为分母相等,所以只要分子相等,即(2/3)x ,因为分母相等,所以只要分子相等,即(2/3)x =2y =2y =(2/5)z =(2/5)z ,(1/3)x ,(1/3)x =y =y =(1/5)z =(1/5)z ,x ,x =3y =3y ,z ,z =5y =5y ,将x ,将x =3y =3y ,y ,y =y =y ,z ,z.gif) =5y =5y.gif) 代入方程,得到y 代入方程,得到y.gif) =±1/3,确定C。 =±1/3,确定C。 |
|
|
3.已知|a|=1,|b|=.gif) ,且 ,且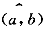 =π/4,则|a+b|等于: =π/4,则|a+b|等于: |
正确答案:D 解题思路:提示:计算|a+b|.gif) =(a+b)·(a+b)=a·a+b·a+a·b+b·b=5。 =(a+b)·(a+b)=a·a+b·a+a·b+b·b=5。 |
|
|
4.球面x.gif) +y +y.gif) +(z+3) +(z+3).gif) =25与平面z=1的交线的方程是: =25与平面z=1的交线的方程是: |
正确答案:D 解题思路:提示:空间曲线方程用两曲面方程联立形式表示。即把z=1,x.gif) +y +y.gif) +(z+3) +(z+3).gif) =25联立,消z得x =25联立,消z得x.gif) +y +y.gif) =9,故在z=1平面上的曲线方程为选项D。 =9,故在z=1平面上的曲线方程为选项D。 |
|
|
5.Ω是由曲面z=x.gif) +y +y.gif) ,y=x,y=0,z=1在第一象限所围成的闭区域,f(x,y,z)在Ω上连续,则 ,y=x,y=0,z=1在第一象限所围成的闭区域,f(x,y,z)在Ω上连续,则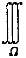 f(x,y,z)dV等于: f(x,y,z)dV等于: |
| 正确答案:C 解题思路:提示:确定Ω在xOy,平面上投影区域的图形,写出在直角坐标系下先z后x最后y的三次积分。 |
- 2012年岩土工程师考试基础知识模拟试题:工程地质(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:理论力学(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:高等数学(单项选择题3)
- 2012年岩土工程师考试专业知识考前冲刺(五)上午卷
- 2016年岩土工程师考试《综合知识》冲刺练习(4)
- 2012年岩土工程师考试基础知识模拟试题:弹性力学和结构力学(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(3)
- 2012年岩土工程师考试基础知识模拟试题:电工与电子技术(单项选择题2)
- 土工结构、边坡与支挡结构、基坑与地下工程(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(5)

